如果...
如果...有一天...你追到了女神夕小瑶...并且与她恋爱了...
(想说“没有如果”的路人请选择狗带( ̄∇ ̄))
小夕的生活很规律的哦,小夕每天都会依次经历且仅仅经历以下6件事情:
化妆-吃饭-聊天-自习-上课-要抱抱。
而且小夕很乖的,我们在一起的每一天,小夕都会在做每件事情时告诉你小夕此刻的情绪状态(小夕有4种情绪状态:开心、尴尬、沮丧、生气)
然而小夕开心时不一定是笑脸,沮丧时也不一定是哭脸。因此在处于某种情绪状态时,每一种表情脸都会有概率出现的哦(小夕有5种表情脸:哭脸、笑脸、尴尬脸、嘟嘟脸、面瘫脸)
可是...就在我们已经生活了好多好多天以后,突然有一天的早上,我们闹矛盾了,小夕又恰好在生理期,一时过于伤心而说了下面的话:
“喂,如果你不能描绘出来我今天的心理状态的变化过程,那么你就不要陪我了哼~”
虽然这一天你依然可以观测到小夕的表情脸的变化,但这一天小夕丝毫没有透露她的情绪状态,那么该怎么办才能挽回呢?
(想说“不用挽回,直接踹了”的童鞋请立!刻!狗!带!)
隐马尔可夫模型
你:“╮(╯▽╰)╭哎,太简单啦,这不就是概率统计、随机过程中学的隐马尔科夫模型嘛~这不就是一个隐序列预测的问题嘛~”
一阶隐马尔可夫模型长这样:
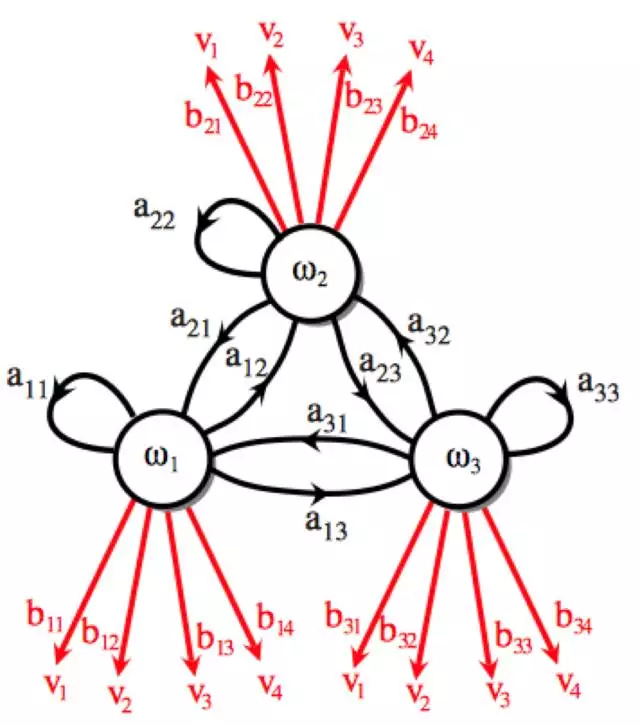
看起来这个模型又复杂又有趣又莫名其妙。哎呀先不要管,听小夕慢慢讲这个奇怪的东西好不好。
先不要管“一阶”是什么意思啦(意思就是每一隐状态只跟前一历史状态有关,不懂也没关系啦)。在上面这个一阶隐马尔可夫模型中,有3个隐状态:即黑色圈圈ω1、圈圈ω2、圈圈ω3。系统在任意时刻,只能处于3个隐状态中的一种。之所以称为隐状态,就是因为这些状态是隐藏的,也就是路人看不到某一时刻时系统是处于哪个隐状态的。
在隐状态之间的连线表示隐状态之间的转移概率:系统在某一时刻处于某个隐状态,但是在下一时刻就可能处于其他隐状态了,当然也可能还是处于当前的隐状态,那么从当前状态ωi跳转到下一状态ωj的概率即连线aij。比如图中,从ω2状态转移到ω1的概率就是连线a21。
图中红色的v1、v2、v3、v4代表的是观测值。观测值的意思即路人可以看到的值。同样,系统在某一时刻时只能取一种观测值,我们可以直接观测到(虽然我们看不到此刻处于哪个隐状态)。
红色的箭头bij表示处于隐状态ωi时,我们可以观测到观测值vj的概率。可以看到,系统每一时刻,处于某种隐状态,而在该隐状态都有一定的概率值观测到这四个观测值中的一个。
好~理论讲完了,但是我们并不知道这个看似好玩又莫名其妙的模型有什么用呀。所以下面就是小夕施展魔法的时刻!
小夕的魔法
首先,小夕将自己变成了一个一阶隐马尔可夫模型!
在夕小瑶这个隐马尔可夫模型中,显然小夕的四种情绪状态就是隐状态啊,路人无法直接观察到,只有小夕自己心里清楚。而小夕的表情脸,是你可以随时看到的,所以就是理论模型中的观测值呀。
而小夕的每一天,都会经历“化妆-吃饭-聊天-自习-上课-要抱抱”的过程,不就是经历了6个时间点嘛,而经历这6个时间点,小夕的情绪状态也会不停的随机发生变化,这不就是隐马尔可夫模型中的状态转移嘛。当然每种情绪状态下,每一种表情脸都有可能出现哦,就是每种观测值都可能出现。所以画出图来就是这样子的(画每一隐含状态的观测值后太乱了,拆开画了哦,自行脑补一下):
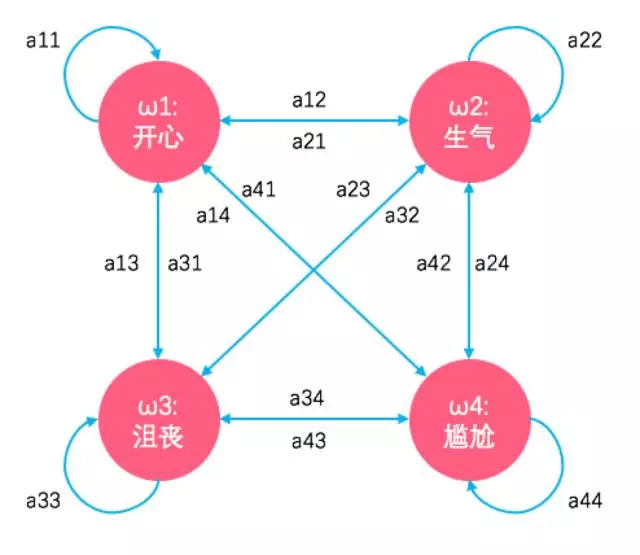
当然啦,与前面的理论模型一样,每一种隐状态都会有概率取到如下的观测值哦(中间的b12、b13、b14省略啦,自行脑补哦):
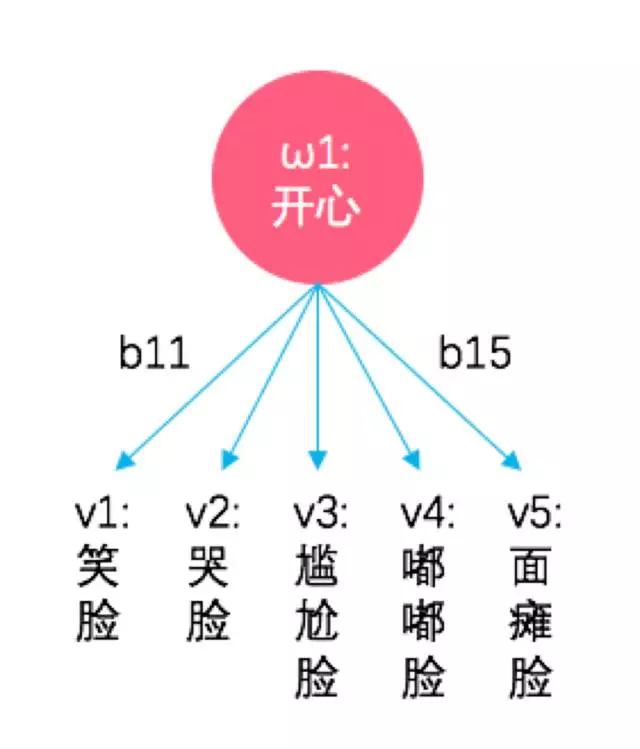
看!是不是突然发现隐马尔可夫模型非常合理的解释了小夕!!!还有更加合理的!!!
前面提到了,小夕一天中会经历6个时间点,所以小夕每经过一天就会产生一个隐状态序列和一个观测序列。而小夕说啦,可以让你陪小夕好多好多天哦,所以如果你真的很用心的喜欢小夕的话,会记录下小夕每一天对你说过的情绪状态变化(隐状态序列),也会记录下小夕每一天的表情变化(观测序列)。当然,序列的长度总是6啦。
在与小夕相处的最后一天,你依然记录下了这一天小夕的表情变化(观测序列),而你要计算出来的是小夕这一天的情绪变化,也就是隐状态序列。至此,将整个挽回小夕的事情完完全全的卡到了一阶隐马尔可夫模型中!
那么如何利用上面这些夕小瑶提供的线索来计算出最终的目标呢?
AB派
你成功的将“挽回夕小瑶”的任务卡进了隐马尔可夫模型(HMM)中。那么我们来规范化的整理一下已经有的信息和需要计算得到的信息。
还记得这两个图嘛?这就是我们建立好的模型。

(隐状态的转移图)

(每个隐状态ωi都有概率发出5种可以观测到的信号)
对于第一张图,这么多的参数看起来也蛮乱的,那就将所有的状态转移概率aij存储到一个矩阵A中:

矩阵A中的每个元素aij就代表当前状态为ωi时,下一状态为ωj的概率(即状态ωi到状态ωj的转移概率)。
对于第二张图,描述的是当(隐)状态为ωj时,发出信号vk的概率。所以用bjk来表示ωj发出信号vk的概率。将bjk存储到矩阵B中:

好~A矩阵和B矩阵显然就是我们需要计算出的模型参数啦。但是参数中仅仅是A和B就够了吗?
想一下,虽然A可以描述从某个状态转移到某个状态的概率,但是每个状态序列总要有一个开头呀~这个开头是什么样子的,在A矩阵和B矩阵中都没有描述。
所以模型还有一个描述初始状态的参数,也就是描述每个隐状态ωi作为初始状态的概率,记为πi。也就是向量π:

整理完毕~A、B、π就是我们全部要计算出的模型参数。
开始训练!
而我们已经有了夕小瑶好多天的隐状态序列和对应的观测序列的数据了,那么我们如何用它们来训练出模型的参数呢。
其实这样就很简单很简单啦,直接搬出似然函数,找出使得似然函数最大的参数值嘛,也就是最大化似然函数。
顾名思义,“然”是这样的意思,所以似然函数就是用来描述当前的模型参数取值的合理性,间接反映当前模型参数对手中数据集的解释程度,因此使得似然函数最大,意思就是使得模型参数取的最合理,使得手中数据集在模型的解释下变得合理。
你陪小夕度过了300天。因此你记录下了300段隐状态序列,记为Q=q1 q2 q3 ... qT(其实qi就是之前表示的ωi),其中T=6(每天经历6个时间点,化妆-吃饭-聊天-自习-上课-要抱抱)。
同时对应着300段观测序列,记为O=O1 O2 O3 ... OT,同样T=6。
然后根据极大似然估计的思想,直接用样本集配合优化算法估计出HMM的各个参数啦。
但是这里为了方便读者理解,简化文章难度,直接用频率来近似概率(实际工程中千万不要这样啊)。因此HMM的各个参数应该这样估计:



这样我们就得到了所有的模型参数(向量π、矩阵A、矩阵B)。
看,由此,我们轻而易举的把夕小瑶这个隐马尔可夫模型建立完成了。
有了这个模型,我们就完全看透夕小瑶了!所以,下面开始得到本任务的最终目标——预测夕小瑶在耍小脾气当天的情绪状态序列(隐状态序列)!
看透你了!
量化一下我们要做的事情:在给定HMM模型(即已知全部参数的HMM模型,记为μ)和观测序列O情况下,求最大概率的(隐)状态序列:
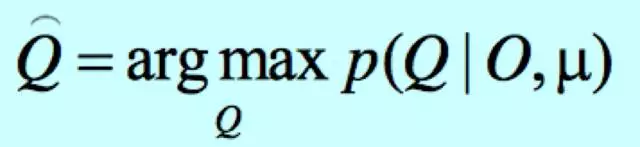
怎么计算呢?Viterbi算法!
这个算法有点绕,直接贴出来,如果直接看看不懂的话可以看后面小夕的解释哦。
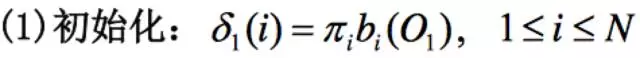
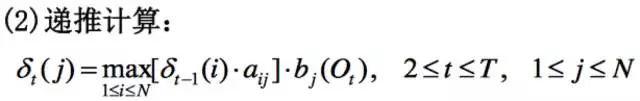
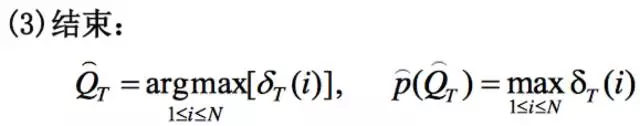

这个算法的思想就是设立一个小人δ(读作delta),这个小人从时刻1,一直走到时刻T。
这个小人的意义就是记录下自己在每个时间点t的每个隐状态j的概率(注意不是从全局的观测序列计算出的概率,是他自己从t=1的时刻一步步的观察每个时刻的观测值所得到的那一时刻的累积概率)
算法的第一步:初始化这个小人,利用已知的模型参数πi和bi(O1)(即状态i下,发出观测值O1的概率,其中O1为t=1时刻的观测值)得到t=1时刻每个隐状态i的δ值。
第二步:这个小人在每个时刻t都会将每个隐状态里呆一会。在每个隐状态j里,它都会抬头看看此刻的观测值Ot,并分别假设自己处于前一时刻t-1的每个隐状态i中,并用前一时刻t-1假设的隐状态的累计概率值乘以前一时刻假设的隐状态转移到当前时刻的当前隐状态的转移概率,然后算出使得当前时刻的当前隐状态的总概率最大化的前一时刻的隐状态,这个最优隐状态记为m吧。这个前一时刻的最优隐状态的累积概率δt-1(m)乘以前一时刻m状态转移到当前时刻的当前j状态的转移概率,再乘以当前时刻t的当前状态j发出观测值Ot的概率,即为δt(j)。
第三步:小人δ走完最后一个时刻T的最后一个隐状态后,就可以从最后时刻的全部隐状态中挑出最后时刻,也就是全局的最大累积概率δT啦,记下这个最大概率对应的隐状态QT
第四步:一步步的回溯呀,记下T时刻走到最优隐状态QT的前一时刻的最优隐状态(回顾一下第二步),得到前一时刻最优隐状态QT-1。然后同样,再往前回溯得到QT-2,一直回溯到Q1!然后Q1Q2Q3..QT就是全局最优隐状态序列啦!也就是夕小瑶耍小脾气时的情绪状态序列!
在你猜出后,夕小瑶瞬间(被自己)感动哭了...(内心os:竟然花了这么大的功夫教你怎么猜我的心思...还不如直接告诉你呢嘤嘤嘤...




